图为真·Paxos———位于希腊的岛屿

如果想要在后端开发上更进一步而不是局限于SSM框架，那么分布式是一个不那么坏的发展方向。如果要研究分布式系统，Paxos算法是绝对绕不过，也不能绕过的知识点。

Leslie Lamport在1998年在《The Part-Time Parliament》中提出了Paxos算法，单单从论文名字看也知道这是篇不怎么正经的论文，这一结论在看完论文后又得到了印证。作者在论文中虚构了一个叫做Paxos的希腊城邦，这个城邦以议会作为最高权利机构，每条法令都需要在此议会中通过后方可实施，作者又对其中的细节作了一些描述和规定，以此符合分布式系统的实际模型。但是，这篇寓言性质的论文对于母语中文的我来说实在过于难懂，哪怕参考了许多资料和解释以后，我仍然很难理解这种模型，就算是读了《Paxos Made Simple》，也很难将其与这个故事一一对应起来。所以，我决定跳过这篇论文，从《Paxos Made Simple》开始说起。

为什么需要Paxos

在开始谈Paxos细节之前，我想有必要谈谈为什么我们需要Paxos。几乎所有的资料都在说Paxos是一种共识性（Consensus）算法那么什么是共识呢，共识性和一致性（Consistency）有什么差别，为什么我们需要共识呢？我希望通过下面的例子解决这个问题。

假设我们开了家“肥宅”奶茶店，为了简化模型，店里只卖珍珠奶茶，我们的配方为奶茶之比为1:1。如果只有一家店，自然是我们说了算。但是有人看我们开得不错，提出要入伙一起干，也不管我们同不同意，总之我们现在有两家店了。作为商业机密，配方是不能透露的，这家店老板也没多想，配方就定了奶茶比为2:1。那么此时，分歧就出现了，也就是说，两家店没有在奶茶的配方上达成“共识”。在这种情况下，由于没有“共识”，消费者在两家“肥宅”奶茶店买到的奶茶竟然味道不同，这就产生了“一致性”的问题。

将上述的奶茶店换成计算机，配方换成提议，奶茶换成数据，就变成了分布式系统的模型。在奶茶店模型中，消费者喝到味道不同的奶茶倒是小事，但是如果在银行系统中，一台机器上余额是一百万，一台是负一百万那问题就大了。而且，由于现在绝大多数业务都需要保证数据一致性，那么保证提议的共识性就显得格外重要了。

Basic Paxos

鉴于有很多朋友也像我一样无法理解《The Part-Time Parliament》，作者在2001年又发了《Paxos Made Simple》重新解释Paxos算法。作者在这篇文章中，终于用能看得懂的英语解释了Paxos算法是怎么运作的。

通读全文，我们可以知道Paxos有两个目标安全性（Safety）和活跃性（Liveness）。其期望分别如下（此处采用Raft作者的理解）

安全性

• 每次提议仅有一个值被选定
• 服务器在值被接受前不会知道该值已被选定

活跃性

• 在一些提议中，最后必定有值会被选定
• 如果值被选定了，那么服务器最后总会知道该值

为了实现以上目标Paxos提出了两条约束，并通过数学证明：任何遵循这两条约束的系统都能保证共识性，此处我们仅讨论在文中作者如何推导出两条约束，不讨论数学上如何证明。该算法中，提议（Proposal）具有两个属性，编号（Number）和值（Value），算法中的规定的角色如下

提议者（Proposer）:负责提出提议

接受者（Acceptor）:负责审阅提议并决定是否批准

学习者（Learner） :不参与议案过程仅学习通过的提案

考虑最简单的情况，我们仅使用一台机器作为Acceptor且接受Number相同的第一个Proposal，那么所有的提议都会由它审阅，并且只会有一种结果，能够保证共识。但是一旦这台机器宕机，那么整个系统就无法继续运行。所以使用多个Acceptor是必要的。此时，仅当Proposal被大于一半的Acceptor接受，该Proposal才被视为通过。虽然在文中此条件没有被显式地列为约束，但我认为其重要程度与后两者相当，因此我将其列为P0

P0：当且仅当Proposal被大多数Acceptor接受（Accepted），该Proposal才被视为选定（Chosen）

为了能保证Paxos 在一个Proposer和一个Acceptor的情况下工作，即符合活跃性的第一条要求，我们提出下面的方案作为约束：

P1：Acceptor必须接受其收到的第一个Proposal

然而此约束存在一个问题，假如几个Proposal同时提出，且被分别发送发不同的Acceptor，每个Acceptor都接受一个Proposal，那么就会出现人均一票的情况，无法形成符合P0的情况，Paxos并未提出如何解决这一问题，而Raft使用随机等待的办法解决此问题。

由P0的约束可知，需要大多数Acceptor接受提案，而P1则要求Acceptor接受其收到的第一个Proposal，那么这就要求每个Acceptor需要接受多个Proposal。这里，我们使用Proposal的Number作为区分。而为了保证被选中的Proposal具有相同的Value，我们提出以下约束：

P2：如果Number为n，Value为v的Proposal被选中，那么所有被选中且Number > n的Proposal都具有Value v

由于Proposal被选中意味着Proposal被大多数Acceptor接受，所以可以进一步约束为

P2a：如果Number为n，Value为v的Proposal被选中，那么所有被接受且Number > n的Proposal都具有Value v

现在，我们假设一个新的 Proposer 刚刚从崩溃中恢复或加入此系统,并且发送了一个带有不同 Value 且Number更高的Proposal。P1要求Acceptor接受这个 proposal，但是却违背了 P2a。为了处理这种情况，需要继续加强P2a，于是我们得到

P2b：如果一个Value为v的Proposal 被选中，那么之后每个 Proposer 提出的具有更大Number的Proposal都有Value v

P2b通过强制要求新的Proposal的值中含有Value解决了上述的问题。而作者通过数学工具，证明以下约束能够满足P2b

P2c：对于任意的Value v和Number n，如果Value为v且Number为n的Proposal被提出，那么一定有多数Acceptor集合S满足：（a）S中不存在Acceptor已经接受任何Number小于n的Proposal，或者（b）S中的Acceptor所接受的Proposal中Number最高的具备Value v。

文中根据P2c将整个流程划分为两段：准备（Prepare）和接受（Accept），但是主要是针对Proposer的，为了适应这个流程，进一步将P1约束如下

P1a：如果Acceptor没有在Prepare阶段回复过Number大于n的请求，那么在Accept阶段，它可以接受Number为n的Proposal

在得到上述的两个约束后，我们就能够以此为依据，得到具体的算法流程。

2 Phase Commit

上文提到整个算法流程分为两个阶段，下面我们将介绍具体流程是怎么样的。

阶段一为准备阶段，具体如下

1. Proposer 选择一个Number n，然后向大多数Acceptor发送Number 为n的Prepare request。
2. 如果一个Acceptor接收到Number为n的Prepare request，并且n大于任何它已经回复的Prepare request的Number，那么它将承诺不再接受任何Number 小于 n的proposal，并且回复已经接受的最大Number的 proposal。

阶段二为接受阶段，具体如下

1. 如果Proposer 接受了来自大多数Acceptor对它的Prepare request 的回 复，那么接下来它将给这些 Acceptor发送Number为n，Value为v的 Proposal作为Accept request。其中v是收到的回复中最大 Number 的Proposal的Value，或者如果回复中没有Proposal的话，就可以是它自己选的任意值。
2. 如果 Acceptor 收到一个Number 为n的Accept request，如果它没有对Number 大于n的Prepare request进行过回复，那么就接受该Accept request。

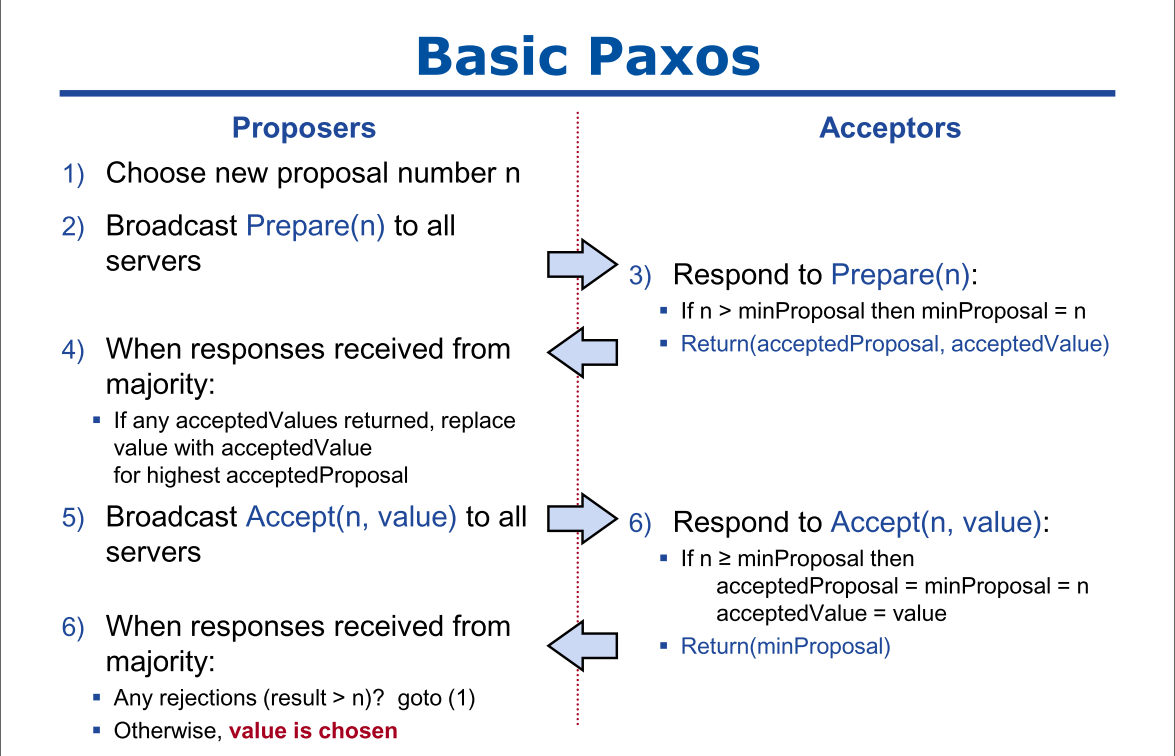
Raft作者的这张图形象地展示了Paxos的整个流程

对Paxos的一些思考

上述内容本质是对《Paxos Made Simple》的翻译和复述，下面我想谈谈我对这个算法一些思考。

我仍然用上文奶茶店的例子，共识指的是两者对同一奶茶的配方认可，一致是奶茶的味道相同。初始奶茶店希望分店和自己采用相同的配方，这个过程就是寻求共识，如果分店同意，那么他们就达成了共识，这一阶段对应于提出Proposal。得到配方后的分店按配方制作奶茶，就能得到和初始奶茶店一样的味道，就相当于保证了数据的一致性。如果采用复制状态机的方案，奶茶配方在计算机系统中就是指令，两台初始完全相同的机器，在以同样顺序执行相同的指令后，就会得到一致的数据。也就是说，只要保证各机器对执行指令和顺序的共识，那么我们就能保证数据的一致性。

为什么Paxos需要P0？

这个约束有两个作用，一是在拥有2f+1台机器的系统中，它能够允许f台机器同时崩溃，而仍能正常处理请求。其次，我们来考虑有2f+1个机器，而我们仅需要f个机器接受请求，那么假如所有的请求和数据都由前f个机器处理，而后f+1个机器没有任何数据。此时，前f个机器崩溃了，那么，我们的系统中就没有任何的数据了。但是，假如是要求f+1个机器接受请求，那么任何两次请求都必然有至少一个机器接受了两次请求，也就是说，它存有全部的最新数据。使用数学归纳法可以得知，无论接受了多少次请求，f+1个机器中所有的存储的数据可以拼接成完整的全部数据，那么，即使f个机器崩溃了，也能保证数据的完整。

总得来说，Quorum机制能保证在2f+1台机器中f台机器崩溃的情况下保证Paxos协议的正常运行和数据的完整性。

为什么Basic Paxos只能处理“Single Decree”？

我们可以看到，如果Proposal希望能被接受，那么他必须包含之前所有被接受过的Proposal的Value，这在实践中是不可能实现的。另外，由于Basic Paxos允许多个Proposer，那么每个Proposal的Number大概率是不一致的，在跨事件的情况下，不能根据自增的Number来判断是否多个Proposal是对一个事件的共识。最重要的是，恐怕作者这篇论文的目的也仅仅是为了解决单个事件的共识。

以前看这篇的论文的时候，由于之前了解的都是有Leader的系统，Proposal的不同Number的代表对不同Value的共识，然后在读Paxos时也代入了这种想法，就不能很好理解Paxos算法，现在从这个角度来看就容易理解得多。同时也可以解释为什么P2a和P2b中要求大Number应包含小Number有的Value，因为此时并不是两个事件，而是对同一事件的修改。比如两次的Value分别是{x=1}和{x=1，y=2}，那么实际上后者只是对前者的补充而已。

为什么需要Prepare阶段?

Prepare阶段主要是为了实现Proposer的共识，这也是和有Leader系统非常不同的一点。

假设三个Proposer有三个版本的Proposal，具体如下

Proposer1：{Number：1，Value：[X=1] }

Proposer2：{Number：2，Value：[X=1，y=2] }

Proposer3：{Number：3，Value：[X=1]，y=2，z=3] }

如果Proposer3最先到达Acceptor，那么根据Prepare阶段的要求，由于Proposer1和Proposer2的Number小于Proposer3，他们会被一直拒绝直到其内容和Proposer3相同。如果Proposer3最迟到达Acceptor，那么Proposer1和Proposer会在Acceptor阶段被拒绝。这里我们假设了Proposer3的Proposal是被选定的情况，如果它不是最终版本，那么，很有可能会出现Value中继续添加值的情况，然后Proposer3也会在第Accept阶段被拒绝，要求它重新提案。

总之，由于Basic Paxos允许多个Proposer存在，所以需要Prepare阶段保证提案的一致性。

为什么我们不使用Basic Paxos？

由于Basic Paxos需要Prepare阶段保证提案的一致性，而且一次算法的运行只能允许完成单次操作，所以如果直接使用Basic Paxos在性能上很可能会达不到我们的要求。因此，学界提出了更加符合实际的Multi-Paxos，使用Basic Paxos选举Leader，让Leader直接提案代替Prepare阶段，从而大大缩短了一次算法运行需要的时间。